Restricted Boltzmann Machine
受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)是由Hinton和Sejnowski于1986年提出的一种生成式随机神经网络(generative stochastic neural network)。由于deep learning的基本网络结构DBN可以用RBM堆叠而成,所以这里先介绍RBM。
RBM是一个能量模型,当一个事物到达稳定状态时,它的能量是最少的。所以一旦知道模型的能量函数,就能够将模型问题转化为函数优化问题。
RBM网络如下图所示:
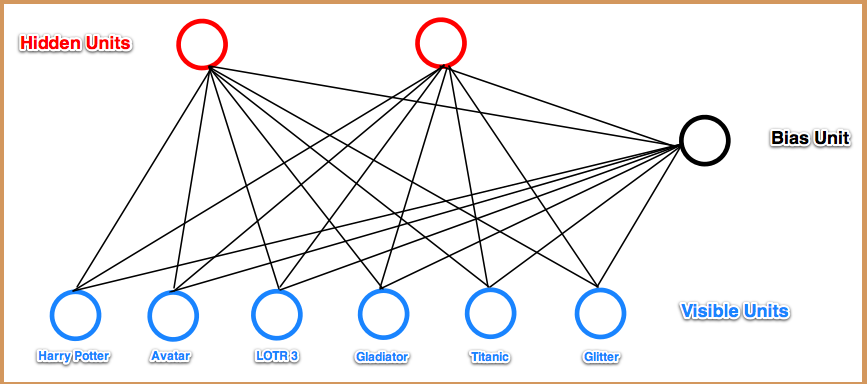
可以看出,RBM网络主要有两层,输入层(也叫可视层)和隐含层(也叫特征提取层)。为了简单起见,在本文中,将网络中的所有神经元都看成是2值的(0, 1)。首先给出该模型的能量方程:
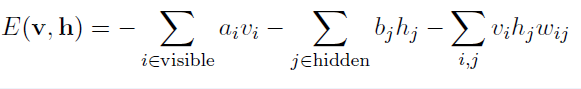 (1)
(1)
这里vi, hj分别表示可视层和隐含层单元的二值数值,ai, bj表示他们的bias,wij是两者连接边的权重。
通过能量函数,网络为每个可视层向量和隐含层向量对分配一个联合概率:
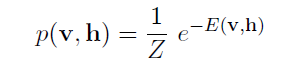 (2)
(2)
Z是归一化因子,也叫partition function:
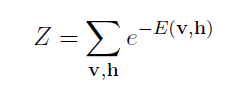 (3)
(3)
根据公式(2),可以得出可视层的边缘概率为:
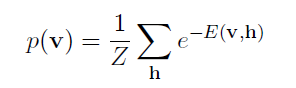 (4)
(4)
由于上面的v是真实的training data,所以我们希望它的值能尽可能的大。从上式可以看出,为了到达这一点,可以调整wij, ai, bj, 以到达降低当前输入向量的energy(E), 提高其它向量的energy。通过以上分析,我们得到了优化目标函数就是P(v)。对其的log求导可以得到:
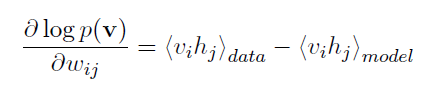 (5)
(5)
其中,<>表示的是均值。<vihj>data表示vihj在训练数据的均值。<vihj>model表示vihj在模型上的均值。
由此,我们可以对wij参数矩阵进行跟新:
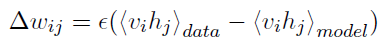 (6)
(6)
其中epsilon是学习率。由于每一层的单元不会与本层单元发生连接,所以单元之间是独立的。对于给定的训练数据向量,可以根据一定的概率得到隐含层的二值概率:
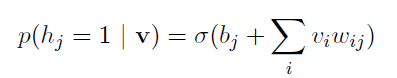 (7)
(7)
这里sigma表示sigmoid激活函数: sigm(x)=1/(1+exp(-x))。
同理,当给定隐含层的输入向量时,也可以得到可视层向量的二值概率:
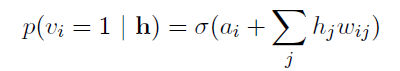 (8)
(8)
根据公式(7),我们可以很容易的得出<vihj>data的值,但是却无法直接得到<vihj>model的值。原因是即使在二值网络模型中,model的组合情况也是2^(|V|+|H|),|V|和|H|分别表示可视层和隐含层的单元个数。这里可以使用Gibbs采样进行估计,但是Hinton在2002年提出了一个更加快速有效的方法:CD(Contrastive Divergence)。
该方法首先初始化可视层状态为一个训练数据向量,然后根据公式(7)计算隐含层单元的二值状态。一旦隐含层的二值状态被确定,又可以根据公式(8)重新构造(reconstruction)输入层二值单元。将此时网络中的二值单元当做是模型的状态。于是wij更新函数可以表示为:
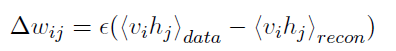 (9)
(9)
重复迭代以上过程知道训练效果到达预期。就可以得到一个RBM网络。
关于RBM的实现可以参考这个python代码。该程序的原网址在这里。
参考文献: