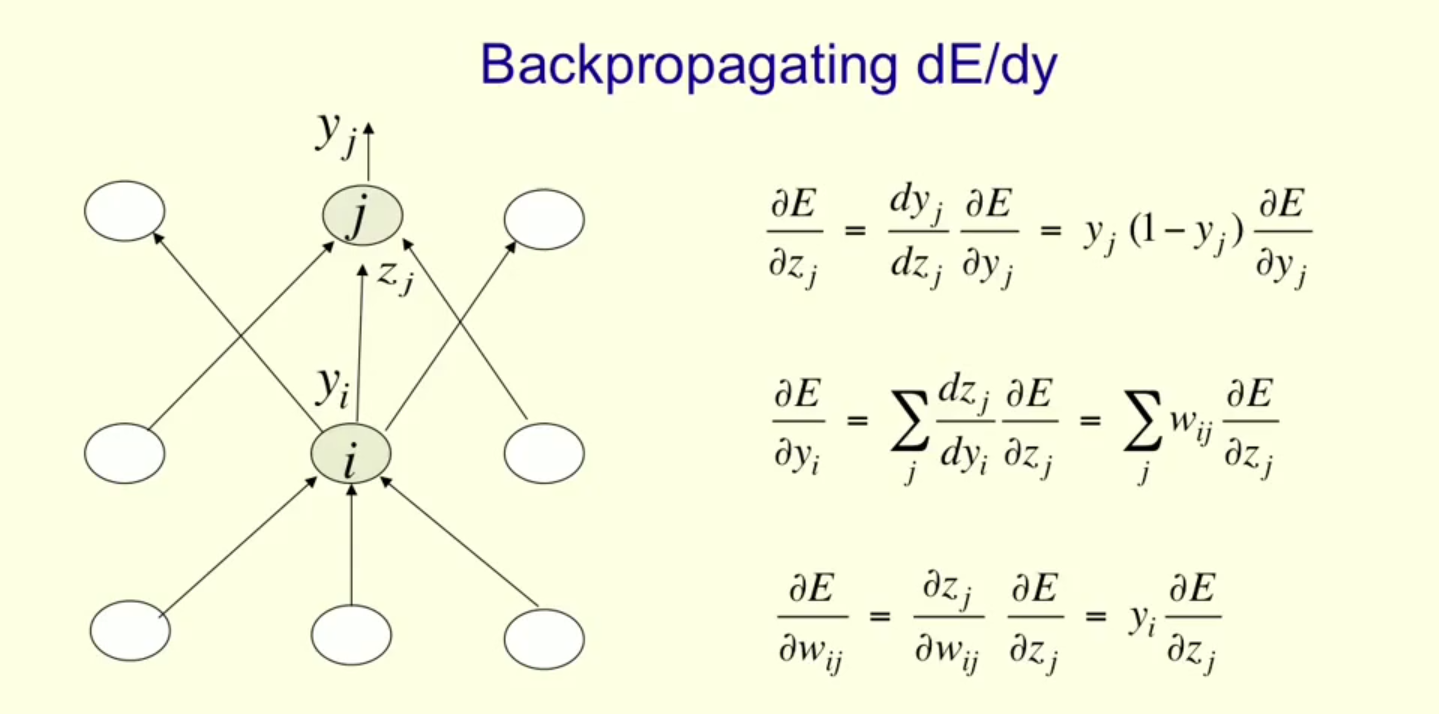
The BackPropagation Algorithm---Neural Network
原始文章见这里
Back-Propagation NN(BP，反向传播神经网络)是一种简单的含隐层(hidden layer)的神经网络，主要由两步完成对数据的训练：
1. 前向传播
前向传播主要是计算在当前的权值参数下，各个神经单元的输出。每个神经单元的输出是上一个神经单元的输出与连接边上权值的线性组合，即输入向量与权值向量的内积。而神经单元的输出则是对输入经过非线性变化的结果，通常采用sigmoid函数进行非线性变换。
每一层上各个神经单元的输出都作为输入输连接到下一层的神经单元
2. 反向反馈
根据前向传播计算的结果，在输出单元上，可以得到输出的误差。根据输出的误差，将其反馈给产生这些误差的神经单元中，对各个神经单元的连接权重进行调整。
在介绍BP之前，先声明几个符号：
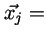表示单元j的输入单元向量（Xji表示输入到j的第i个单元）。
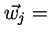表示连接到j单元上的权重向量（Wji表示单元i与单元j之间的权重）。
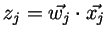输入到j单元上的权重- Oj 表示j单元的输出（
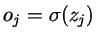） - Tj 表示j单元的目标输出（由训练集中给出）
- Downstream(j) 表示与单元j直接相连的下一层神经单元集合
- Outputs 表示最后一层单元上的输出
由于神经网络的训练过程是针对每个训练集个体的输入进行参数调整，所以这里只需要将训练集看成一个样本简化即可。这里把误差用E进行简单表示。下面介绍参数调整过程。
首先，对于每一个输出单元j，我们希望计算输入权重Wji的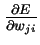
。
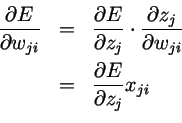
由于无论输入到上j上的需要更新的权重是多少，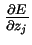
总是一样的，我们把它标记为
。
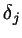考虑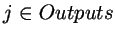 
，我们可以知道：
对于所有的输出单元k，当k不等于j时，输出单元都与Wji想独立，所以我们可以把加和符号去掉，简单的用j上的E进行表示。
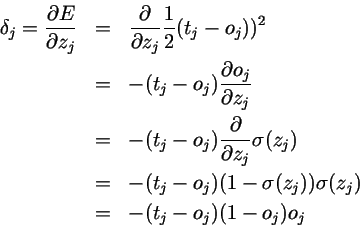
于是：
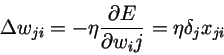
现在考虑当j是hidden layer的单元时。我们首先观察得出以下两个重要的性质：
- 对于每一个属于Downstream(j)的单元k，Zk是关于Zj的函数。
- 同一层中除了j之外的其他所有单元l对最终错误的贡献独立于Wji
同样，对于每一个hidden layer上的单元j，我们希望计算权重Wji的。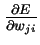
注意到Wji影响Zj进而影响Oj进而影响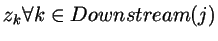
进而影响到了E，所以我们可以得出：
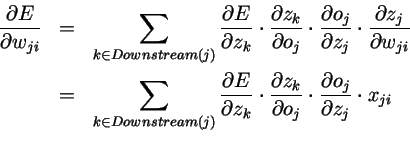
跟上面一样，我们可以把除了上式中Xji意外的项表示为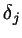。带入得：
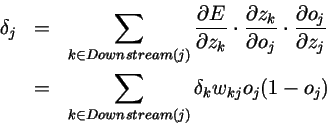
因此可得：
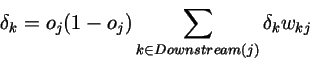
算法的正式描述
- 创建一个包含Ni和输入单元，Nh个hidden单元，No个输出单元的神经网络.
- 初始化各个权重Wji
- 直到满足终止condition：
对于每一个训练样本：
根据输入计算输出
对于每一个输出单元k，计算
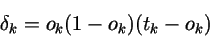
对于每一个hidden layer的单元h，计算：
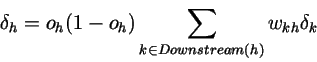
根据下面公式进行更新：
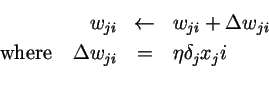
一体化公式见下图：
